"I like this app"
133
Sub Topics
104
MCQs
37
MCOs
80
True/False
43
Fill Blanks
9
Rearrange
38
Matching
16
Comprehensions
42
Flashcard Decks
Curriculum
What You'll Learn
01 Foundations of Real Numbers 3 topics
1 The Real Number System
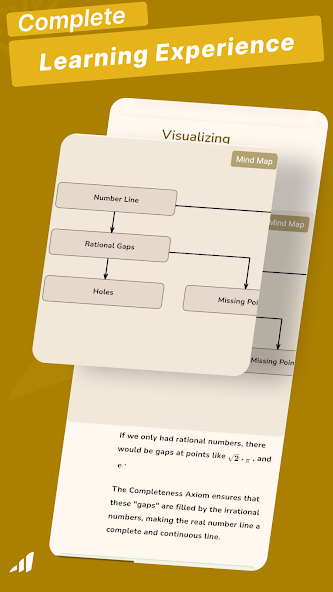
- Axioms and Properties
- Completeness Axiom
- Supremum and Infimum
- Archimedean Property
2 Sequences of Real Numbers
- Convergence and Divergence
- Monotone Sequences
- Bounded Sequences
- Cauchy Sequences
3 Topology of the Real Line
- Open and Closed Sets
- Compact Sets
- Connected Sets
- Cantor Set
02 Limits and Continuity 3 topics
1 Limits of Functions
- Definitions and Properties
- One-sided Limits
- Infinite Limits
- Limits at Infinity
2 Continuous Functions
- Definition and Basic Properties
- Continuity on Intervals
- Uniform Continuity
- Continuity and Compactness
3 Properties of Continuous Functions
- Intermediate Value Theorem
- Extreme Value Theorem
- Preservation of Connectedness
- Preservation of Compactness
03 Differentiation 3 topics
1 The Derivative
- Definition and Interpretation
- Rules of Differentiation
- Higher Derivatives
2 Mean Value Theorems
- Rolle's Theorem
- Mean Value Theorem
- Cauchy's Mean Value Theorem
3 Applications of Differentiation
- L'Hôpital's Rule
- Taylor's Theorem
- Local Extrema
- Convexity and Concavity
04 Riemann Integration 4 topics
1 The Riemann Integral
- Riemann Sums
- Upper and Lower Integrals
- Integrability Criteria
2 Properties of the Riemann Integral
- Linearity
- Additivity
- Monotonicity
- Integrability of Continuous Functions
3 Fundamental Theorems of Calculus
- First Fundamental Theorem
- Second Fundamental Theorem
- Integration Techniques
4 Improper Integrals
- Types of Improper Integrals
- Convergence Tests
- Absolute and Conditional Convergence
05 Sequences and Series of Functions 4 topics
1 Pointwise and Uniform Convergence
- Definitions and Basic Properties
- Cauchy Criterion for Uniform Convergence
- Dini's Theorem
2 Properties of Uniformly Convergent Sequences
- Continuity
- Integration
- Differentiation
3 Power Series
- Radius of Convergence
- Term-by-Term Differentiation
- Term-by-Term Integration
- Analytic Functions
4 Fourier Series
- Trigonometric Series
- Convergence Theorems
- Parseval's Identity
06 Functions of Several Variables 4 topics
1 Topology in R^n
- Metrics and Norms
- Open and Closed Sets
- Compactness
- Connectedness
2 Limits and Continuity in R^n
- Definitions
- Properties
- Uniform Continuity
3 Partial Derivatives and Differentiability
- Partial Derivatives
- Total Differentiability
- Chain Rule
- Implicit Function Theorem
4 Multiple Integrals
- Definition of Double and Triple Integrals
- Fubini's Theorem
- Change of Variables
- Applications
07 Lebesgue Measure and Integration 4 topics
1 Lebesgue Measure
- Outer Measure
- Measurable Sets
- Properties of Lebesgue Measure
- Non-measurable Sets
2 Measurable Functions
- Definition and Properties
- Approximation by Simple Functions
3 Lebesgue Integration
- Definition for Simple Functions
- Definition for Bounded Measurable Functions
- Definition for Unbounded Functions
- Comparison with Riemann Integration
4 Convergence Theorems
- Monotone Convergence Theorem
- Fatou's Lemma
- Dominated Convergence Theorem
- Applications
08 Functional Analysis Elements 4 topics
1 Normed Vector Spaces
- Definition and Examples
- Banach Spaces
- Completeness
2 Hilbert Spaces
- Inner Product Spaces
- Orthogonality
- Orthonormal Bases
- Riesz Representation Theorem
3 Linear Operators
- Bounded Linear Operators
- Operator Norm
- Adjoint Operators
- Compact Operators
4 Applications
- Hahn-Banach Theorem
- Open Mapping Theorem
- Closed Graph Theorem
- Uniform Boundedness Principle
09 Measure Theory Extensions 4 topics
1 Signed Measures
- Jordan Decomposition
- Hahn Decomposition
- Absolute Continuity
- Radon-Nikodym Theorem
2 Product Measures
- Construction
- Fubini-Tonelli Theorems
- Iterated Integrals
3 Lp Spaces
- Definition and Properties
- Hölder's Inequality
- Minkowski's Inequality
- Completeness of Lp Spaces
4 Convergence in Measure
- Definition and Properties
- Relationship with Other Convergence Types
- Egorov's Theorem
- Lusin's Theorem
10 Complex Analysis Foundations 4 topics
1 Complex Numbers and Functions
- Topology of the Complex Plane
- Limits and Continuity
- Analytic Functions
2 Complex Differentiation
- Cauchy-Riemann Equations
- Harmonic Functions
- Power Series Representations
3 Complex Integration
- Line Integrals
- Cauchy's Theorem
- Cauchy's Integral Formula
- Liouville's Theorem and Fundamental Theorem of Algebra
4 Laurent Series and Residues
- Laurent Series Expansions
- Classification of Singularities
- Residue Theorem
- Applications to Real Integrals
Explore More
Real Analysis
Get it on Google Play