Learn multivariable calculus: partials, gradients, multiple integrals
83
Sub Topics
85
MCQs
25
MCOs
59
True/False
32
Fill Blanks
9
Rearrange
32
Matching
16
Comprehensions
29
Flashcard Decks
Curriculum
What You'll Learn
01 Vectors and Vector-Valued Functions 2 topics
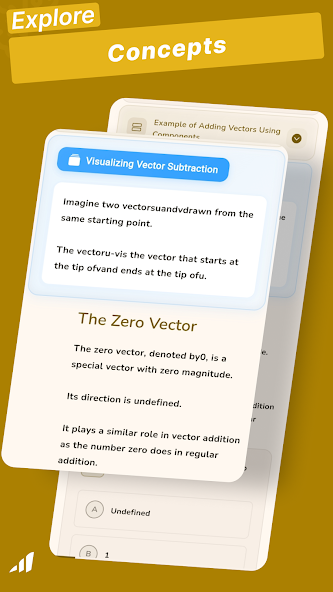
1 Vectors in the Plane and Space
- Vector Operations and Properties
- Dot Product and Applications
- Cross Product and Applications
- Lines and Planes in Space
2 Vector-Valued Functions
- Curves in Space
- Derivatives and Integrals of Vector Functions
- Arc Length and Curvature
- Motion in Space: Velocity and Acceleration
02 Functions of Several Variables 2 topics
1 Introduction to Multivariable Functions
- Domains and Ranges
- Graphs and Level Curves/Surfaces
- Examples of Functions of Several Variables
2 Limits and Continuity
- Definition of Limits in Multiple Dimensions
- Properties of Limits
- Continuity and Discontinuities
- Squeeze Theorem for Multivariable Functions
03 Partial Derivatives 3 topics
1 Partial Derivatives
- Definition and Computation
- Higher-Order Partial Derivatives
- Mixed Partials and Clairaut's Theorem
2 The Chain Rule
- Chain Rule for Functions of Several Variables
- Implicit Differentiation
- Directional Derivatives
3 Gradient, Divergence, and Curl
- The Gradient Vector and Properties
- Directional Derivatives and the Gradient
- Divergence of a Vector Field
- Curl of a Vector Field
- Applications in Physics and Engineering
04 Optimization 2 topics
1 Critical Points and Extrema
- Finding Critical Points
- Second Derivative Test
- Classification of Critical Points
2 Constrained Optimization
- Lagrange Multipliers
- Multiple Constraints
- Applications of Lagrange Multipliers
05 Multiple Integrals 3 topics
1 Double Integrals
- Double Integrals over Rectangles
- Double Integrals over General Regions
- Applications of Double Integrals
- Double Integrals in Polar Coordinates
2 Triple Integrals
- Triple Integrals in Rectangular Coordinates
- Applications of Triple Integrals
- Triple Integrals in Cylindrical Coordinates
- Triple Integrals in Spherical Coordinates
3 Change of Variables in Multiple Integrals
- Jacobians
- Change of Variables in Double Integrals
- Change of Variables in Triple Integrals
06 Vector Calculus 3 topics
1 Line Integrals
- Line Integrals of Scalar Functions
- Line Integrals of Vector Fields
- Work and Flow
- Independence of Path
2 Surface Integrals
- Parametric Surfaces
- Surface Area
- Surface Integrals of Scalar Functions
- Surface Integrals of Vector Fields
- Flux Across a Surface
3 Fundamental Theorems of Vector Calculus
- Green's Theorem
- Stokes' Theorem
- Divergence Theorem (Gauss's Theorem)
- Conservative Vector Fields and Potential Functions
07 Differential Forms and Exterior Calculus 4 topics
1 Differential Forms
- 1-Forms and Covectors
- Wedge Product
- k-Forms
2 Exterior Derivatives
- Definition and Properties
- Relation to Gradient, Curl, and Divergence
3 Integration of Differential Forms
- Orientation
- Integration Over Chains
4 Generalized Stokes' Theorem
- Unified View of Green's, Stokes', and Divergence Theorems
- Applications in Physics and Differential Geometry
08 Applications of Multivariable Calculus 3 topics
1 Physics Applications
- Electromagnetism
- Fluid Dynamics
- Thermodynamics
2 Engineering Applications
- Optimization Problems
- Center of Mass and Moments of Inertia
- Heat Transfer
3 Economics and Finance Applications
- Utility Functions
- Production Functions
- Optimization in Economics
09 Advanced Topics 3 topics
1 Manifolds and Tangent Spaces
- Definition of Manifolds
- Applications in Physics and Geometry
2 Tensors
- Tensor Fields
- Tensor Calculus
- Applications in Mechanics and Relativity
3 Introduction to Differential Geometry
- Curvature of Surfaces
- Geodesics
- Fundamental Forms
- Gauss-Bonnet Theorem
Explore More
Multivariable Calculus
Get it on Google Play